Numerical Mathematics with Applications
Major research interests
Efficient Simulation methods for complex Multiphysics problems.
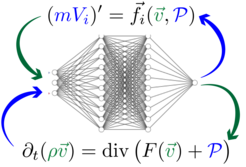
One focus of our group is work on hybrid models that combine (partial) differential equations with neural networks. We develop such complex models for multiphysics problems, study their numerical analysis, and implement efficient algorithms to accelerate simulations.
- Scientific Machine Learning We investigate how neural networks can be used to accelerate numerical simulations of complex and coupled problems described by partial differential equations. We particularly investigate hybrid models and hybrid approaches where classical simulation approaches are augmented with machine learning techniques.
- Adaptive Finite Elements Adaptivity in finite element discretization is a flexible tool for reduction of the problem size. We study goal-oriented error estimators that can be applied to complex systems of equations and that are also transferred to error estimation of temporal discretization schemes.
- Fluid-Structure Interactions We study the interaction of a fluid and an (elastic) solid. In the focus of the research are powerful modelling approaches that are able to handle non-standard problems with large motion and deformation and also to cover (elastic) contact.
- Temporal multiscale modelling Many problems include multiple scales in time, for instance the slow degradation of devices (e.g. hydrogen cells) that is driven by rapidly oscillating loads. Such long-term processes cannot be simulated using classical direct approaches that resolve all scales. We develop efficient numerical multiscale methods that separate the scales and allow for accelerations up to 1:10000.
Possible research projects (not exhaustive)
- Smart flow-based particle sorting of complex waste mixtures
(Collaboration partners: Prof. van Wachem, apl. Prof. Janiga, Prof. Mostaghim, Prof. Benner) - Efficient simulation of particle-laden flows
(Collaboration partners: Prof. Benner, Prof. van Wachem, Prof. Mostaghim) - Model and complexity reduction
(Collaboration partners: Prof. Benner, Dr. Feng, Prof. Sager)
Current doctoral researchers in the IMPRS ProEng program

Dayron Chang Dominguez
PhD project since April 2021: Multirate methods for complex coupled differential equations


