Control of Particulate Processes
Particle formation in fluidized beds represents an important class of processes in the chemical, pharmaceutical, and food industries. The objective is the stable production of tailor-made particles with given product properties. In general, due to the complex interaction between particle growth, heat and mass transfer between the particle and the fluid phase, this is a challenging issue. In practice, product and process development is often dominated by expensive and time-consuming trial and error procedures. Our research aims to achieve a better understanding of the complex dynamics of these processes by using mathematical models and to improve particle formation in fluidized beds by developing new methods for model-based control.
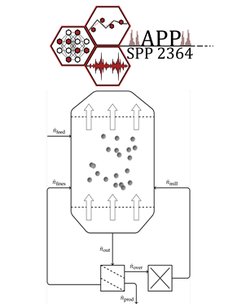
On the large scale, fluidized bed particle processes are operated continuously. For this purpose, they are often equipped with a sieve mill cycle which facilitates product classification and milling of oversized particles. Milled particles are then fed back to the process chamber together with the undersized particles. Depending on the mode of operation, it is possible to distinguish two different types of particle formation processes in the fluidized bed. For agglomeration processes, the injected liquid is a binder which supports the aggregation of particles. For layering granulation, the injected liquid is a solid solution or suspension, which is deposited on the surface of the particles and leads to a layer-wise growth of the particles after drying. In granulation, aggregation of particles may also take place but is usually avoided by carefully adjusting the operating conditions.
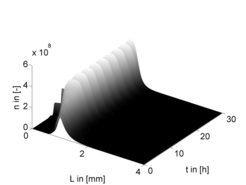
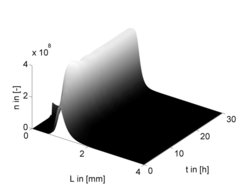
In our research, the initial focus was on layering granulation. The main results related to population balance modeling, dynamics and control have been summarized recently in [1]. In a first step, stabilization of open loop unstable processes with sieve mill cycle (Fig. 1a) by feedback control was considered. A quantitative model for this challenging process was developed and the potential of feedback control for this class of processes was demonstrated experimentally in cooperation with the Heinrich group in TU Hamburg at a large-scale plant [2]. The results are summarized in Fig. 1c. It is shown that the controller dampens the oscillatory behavior of the particle size distribution rapidly and therefore reduces the time until the system settles down to the desired steady state significantly by more than 1 day. Theoretical and experimental results match very well.
Besides particle size, particle porosity is also an important product property in many applications. For pharmaceutical processes, particle porosity is often directly related to dissolubility and efficacy of the drug. It was shown by our cooperation partners from the OVGU that particle porosity mainly depends on the thermal conditions [R1] in the granulation chamber. Hence, an extended mathematical model was developed including the influence of thermal conditions [3]. Subsequently, the model was used to develop an extended cascade control concept to control particle size and porosity [4]. Theoretical results are shown in Fig. 1d. More advanced and more robust control concepts with reduced measurement effort were presented at the IFAC world congress [5,6,7]. An extension to multi-chamber processes was discussed in [8].
More recently, the focus has shifted to agglomeration processes. It turns out that physical modeling is much more difficult for this type of process. The challenge is to capture the effect of various process parameters like binder spray rate, particle feed rate and thermal process conditions on particle morphology in a quantitative way, which is essential for process control. Therefore, we have followed a hybrid modeling approach which combines population balance modeling with data-driven kernel identification. Initially, the focus was on steady state operation [9,10,11]. Results look very promising and can be extended in the future in combination with online identification for the development of new control concepts [12,13].
Cooperation
- Prof. Evangelos Tsotsas, Universität Magdeburg
- Prof. Stefan Heinrich, Technische Universität Hamburg-Harburg
- Prof. Andreas Bück, Universität Erlangen
- Prof. Antos , Politechnica Rzeszowska, Poland
References
[1] C. Neugebauer, E. Diez, L. Mielke, S. Palis, A. Bück, E. Tsotsas, A. Kienle, and S. Heinrich. Dynamics of spray granulation in continuously operated horizontal fluidized beds. In S. Heinrich, editor, Dynamic Flowsheet Simulation of Solids Processes, pages 67–107. Springer Nature, Zürich, 2020.
[2] C. Neugebauer, E. Diez, A. Bück, S. Palis, S. Heinrich, and A. Kienle. Dynamics and control of continuous fluidized bed layering granulation with screen-mill-cycle. Powder Technol., 354:765–778, 2019.
[3] C. Neugebauer, A. Bück, S. Palis, L. Mielke, E. Tsotsas, and A. Kienle. Influence of thermal conditions on particle properties in fluidized bed layering granulation. Processes, 6(12):235, 2018.
[4] C. Neugebauer, A. Bück, and A. Kienle. Control of particle size and porosity in continuous fluidized bed layering granulation processes with sieve mill cycle. Chem. Eng. Technol., 43:813–818, 2020.
[5] C. Neugebauer, C. Seidel, S. Palis, and A. Kienle. Robust control of fluidized bed layering granulation. In Proc. IFAC World Congress - Berlin, July 11-17, 2020. IFAC-PapersOnLine, Volume 53, Issue 2, Pages 11422-11427.
[6] R. Dürr, C. Neugebauer, S. Palis, A. Bück, and A. Kienle. Inferential control of product properties for fluidized bed layering granulation. In Proc. IFAC World Congress - Berlin, July 11-17, 2020. IFAC-PapersOnLine, Volume 53, Issue 2, Pages 11410-11415.
[7] E. Otto, C. Neugebauer, S. Palis, and A. Kienle. Lyapunov-based online parameter estimation for continuous fluidized bed layering granulation. In Proc. IFAC World Congress - Berlin, July 11-17, 2020. IFAC-PapersOnLine, Volume 53, Issue 2, Pages 11398-11403.
[8] S. Palis. Control of multi-chamber continuous fluidized bed spray granulation. In Proc. 12th IFAC symposium on Dynamics and Control of Process Systems - DYCOPS 2019, Florianopolis/Brazil, 23-26 April, 2019. IFAC-PapersOnLine, Volume 52, Issue 1, Pages 406-411.
[9] I. Golovin, G. Strenzke, R. Dürr, S. Palis, A. Bück, E. Tsotsas, and A. Kienle. Parameter identification for continuous fluidized bed spray agglomeration. Pro- cesses, 6(12):246, 2018.
[10] G. Strenzke, R. Dürr, A. Bück, and E. Tsotsas. Influence of operating param- eters on process behavior and product quality in continuous spray fluidized bed agglomeration. Powder Technol., 375:210–220, 2020.
[11] E. Otto, R. Dürr, G. Strenzke, S. Palis, A. Bück, E. Tsotsas, and A. Kienle. Kernel identification in continuous fluidized bed spray agglomeration from steady state data. Adv. Powder Technol., 32:345, 2021.
[12] E. Otto, S. Palis, and A. Kienle. Nonlinear control of fluidized bed spray agglomer- ation processes. In SEMA SIMAI Springer Series, volume 2, pages 73–87, 2021.
[13] E. Otto, J. Behrens, R. Dürr, S. Palis, and A. Kienle. Control of particle processes, 2021. Proc. ADCHEM 2021.
[R1] C. Rieck, T. Hoffmann, A. Bück, M. Peglow, and E. Tsotsas. Influence of drying conditions on layer porosity in fluidized bed spray granulation. Powder Technol., 272:120–131, 2015.

Approaches and results
As particulate processes are typically modeled by population balance equations, i.e. nonlinear integro-differential equations, control design is a challenging issue. Suitable approaches developed in the PSD group can be categorized into two classes:
- Early lumping. Here, the model of the particulate process is lumped applying appropriate discretization schemes. In order to cope with the introduced errors and other model uncertainties robust control methods are applied. [6,7,11,13,15,16]
- Late or no lumping. Applying a generalized stability concept, i.e. stability with respect to two discrepancies, a nonlinear control law can be derived without any model reduction [4,14,17]. In order to account for model uncertainties and time-varying process behavior the discrepancy based control approach can be extended by appropriate adaptation schemes [12]. In addition to the aforementioned discrepancy based control two different control approaches have been developed and investigated for two specific granulation processes: model-free adaptive control based on a discrepancy [2] and control based on thermodynamic quantities [10] guaranteeing closed-loop stability in a classical sense, i.e. in terms of a L2-norm.

Although, population balance models are able to reflect the qualitative process behavior in many applications, modeling errors may be significant. The main two causes are a process specific time-variation of parameters and the deviation between process kinetics and kinetics identified from individual and simplified experiments. In order to overcome this problem a Lyapunov based identification scheme has been developed being able to identify population balance parameters and kinetics online in parallel to the process operation [1,3,9].
Cooperation
- Prof. Stefan Heinrich, Technische Universität Hamburg-Harburg
- Prof. Seidel-Morgenstern, Max-Planck-Institut Magdeburg
- Prof. Evangelos Tsotsas, Universität Magdeburg
- Prof. Richard Braatz, Massachusetts Institute of Technology
- Prof. Andreas Bück, Universität Erlangen
References
[1] I. Golovin, G. Strenzke, M. Wegner, S. Palis, A. Bück, A. Kienle, and E. Tsotsas. Parameter identification for continuous fluidized bed spray agglomeration, 2018. Paper presented at PBM 2018 in Ghent/Belgium.
[2] S. Palis. Non-identifier-based adaptive control of continuous fluidized bed spray granulation. Journal of process control, 71:46-51, 2018.
[3] S. Palis and A. Kienle. Online parameter identification for continuous fluidized bed spray granulation with external sieve-mill cycle. In 22nd Int. Conf. on Methods and Models, Miedzyzdrojie Pl, p. 594–598, 2017.
[4] R. Geyyer, R. Dürr, E. Temmel, T. Li, H. Lorenz, S. Palis, A. Seidel-Morgenstern, and A. Kienle. Control of continuous mixed solution mixed product removal crystallization processes. Chem. Eng. Technol., 40:1362–1369, 2017.
[5] A. Kienle, S. Palis, M. Mangold, and R. Dürr. Modeling and simulation of particulate processes. Electronic Modeling, ISSN 0204-3572, 38(5):23–33, 2016.
[6] S. Palis, C. Neugebauer, A. Bück, S. Heinrich, E. Tsotsas, and A. Kienle. Control of multi-chamber continuous fluidized bed spray granulation, 2016. PARTEC 2016: International Congress on Particle Technology, Nuremberg, Germany, April 19-21.
[7] R. Geyyer, S. Palis, and A. Kienle. Robust control of continuous crystallization processes. In Proc. 1st IFAC Conference on Modeling, Identification, and Control of Nonlinear Systems, Petersburg, June 24-26, 2015. IFAC-Papers-Online, Volume 48, Issue 11, p. 798-603.
[8] S. Palis & C. Dreyschultze & C. Neugebauer & A. Kienle. Auto-tuning control systems for improved operation of continuous fluidized bed spray granulation processes with external product classification. In: Procedia engineering. - Amsterdam [u.a.] : Elsevier, Bd. 102. 2015, pp. 102-133.
[9] S. Palis & R. Dürr & A. Kienle. Online parameter identification of facet growth kinetics in crystal morphology population balance models. In: Procedia engineering. - Amsterdam [u.a.] : Elsevier, Bd. 102. 2015, pp. 1336-1345.
[10] S. Palis, A. Bück, and A. Kienle. Entropy based control of continuous fluidized bed spray granulation processes. In Proc. 5th IFAC Workshop on Lagrangian and Hamiltonian Methods for Nonlinear Control, Lyon, July 4-7, 2015. IFAC-PapersOnline, Volume 48, Issue 13, p. 154-157.
[11] R. Geyyer & A. Kienle & S. Palis, Robust control of continuous crystallization processes, 1st IFAC Conference on Modelling, Identification and Control of Nonlinear Systems - MICNON (St. Petersburg), 2015.
[12] S. Palis, Adaptive discrepancy based control of particulate processes, 1st IFAC Conference on Modelling, Identification and Control of Nonlinear Systems - MICNON (St. Petersburg), 2015.
[13] A. Bück & S. Palis & E. Tsotsas, Model-based control of particle properties in fluidised bed spray granulation, Powder Technology, 2015, pp. 575–583.
[14] S. Palis & A. Kienle, Discrepancy based control of particulate processes, Journal of Process Control 24, 2014, pp. 33-46.
[15] S. Palis & A. Kienle, H infinity Loop Shaping Control for Continuous Fluidized Bed Spray Granulation with Internal Product Classification, Ind. & Eng. Chem. Research, 2013, pp. 408-420.
[16] S. Palis, A. Kienle, Stabilization of continuous fluidized bed spray granulation with external product classification, Chemical Engineering Science 70:200-209, 2012.
[17] S. Palis, A. Kienle, Diskrepanzbasierte Regelung der kontinuierlichen Flüssigkristallisation, at- Automatisierungstechnik 60, 2012, pp.145-154.




