Elementary Process Functions (EPF) Methodology
State-of-the-art methods for chemical process design are (i) experience-based and model-supported heuristics which are easy to apply and lead to reasonable results, at least for not too complex systems; (ii) attainable region concepts which typically make use of predefined ideal reactors to find an optimal reactor network, but are hard to apply to processes with integrated recycles; (iii) rigorous optimization methods in which either superstructures of units are optimized, where MINLP problems are to be solved, or dynamic programming approaches from which optimal temperature and concentration profiles along the reaction coordinate can be found. The main drawback of most approaches is the reliance and need of a predefined set of process units from which the design task is solved. Thus, these approaches are limited with regard to the design of innovative and possibly integrated process (units) and networks which requires an alternative view on the design problem.
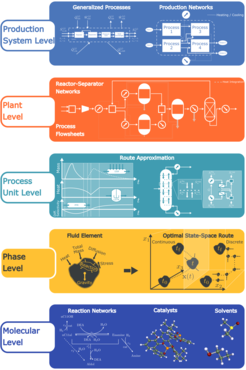
In 2008, the PSE group proposed a novel methodological approach, the Elementary Process Functions (EPF) methodology, for the optimal design of chemical production processes. An illustration can be found in the Figure below [1,2]. In its original form, the EPF approach is based on the idea that in each chemical process Lagrangian matter elements are manipulated along their travel route through the process by the action of mass, energy, and momentum fluxes according to one or multiple objective functions. In terms of the process hierarchy, the consideration of matter elements is linked to the phase level. At this level, independent of specific devices or unit operations, we are able to determine an ideal process route via dynamic optimization at unlimited fluxes but with predefined system-inherent constraints, provided that we have access to adequate knowledge about the reaction kinetics. Then, the ideal process route is approximated on the process unit level by the application of a combination of existing devices or new tailor-made equipment. This is achieved in a three-step procedure under consideration of many alternatives [3] including the operation mode (semi-batch, repeatedly-operated semi-batch [4,5] or continuous operation [6]).
In recent years, we have further extended the EPF process design concept in various key areas. On the Process Unit Level, a probabilistic approach was introduced to quantify the influence of parameter uncertainties on the process design and to increase the robustness of the optimal design solutions [7]. As the axial dispersion properties of different reactor types significantly impact the reaction performance, a systematic and efficient framework was introduced to incorporate back-mixing, substrate dosing and process-wide recycling in the EPF calculations. In addition, an alternative approach to the interpretation of the control profiles in the form of a Flux Profile Analysis was developed. By analyzing the optimal mass and energy control fluxes of a dynamic optimization of a (semi-)batch process, reactor (recycle) network candidates can be synthesized, bridging the conceptual gap between dynamic optimization of batch reactors and the superstructure-based synthesis of continuously operated reactor networks [6,8]. Finally, first approaches to the design of reactor separator networks were studied [9].
An alternative view on the EPF methodology is presented in the FluxMax approach which can be applied to nearly all process system levels such as the Phase, Process Unit, Plant as well as Production System Level. In this approach, the state space itself is discretized into thermodynamic state, elementary process and utility nodes instead of operating on the dynamic trajectory of the matter element. Together with the edges connecting the nodes and representing the different fluxes, a directed graph and, consequently, a thermodynamic network flow optimization problem can be formulated [10–12]. The calculation of the thermodynamic potentials (enthalpy, entropy, Gibbs energy) of the state notes as well as additional non-linearities are decoupled from the solution of the network flow optimization problem, leading to a convex solution space and a globally optimal process design solution in case of a convex (or convexified) objective function. In addition to the design of optimal reactor units, exemplified on the production of methanol [10], the FluxMax approach was successfully applied to the synthesis of a complete and novel process for the production of hydrogen cyanide [11] and the design of separation units, in particular distillation columns, while simultaneously incorporating heat integration considerations [12–14].
Publications
[1] H. Freund und K. Sundmacher, „Towards a methodology for the systematic analysis and design of efficient chemical processes“, Chem. Eng. Process. Process Intensif., Bd. 47, Nr. 12, S. 2051–2060, Nov. 2008, doi: 10.1016/j.cep.2008.07.011.
[2] K. Sundmacher und H. Freund, „Chemical Process Design: Moving Matter Elements along optimal travel routes in the Thermodynamic State Space“, Asia, 2010, S. 1–7.
[3] A. Peschel, H. Freund, und K. Sundmacher, „Methodology for the Design of Optimal Chemical Reactors Based on the Concept of Elementary Process Functions“, Ind. Eng. Chem. Res., Bd. 49, Nr. 21, S. 10535–10548, Nov. 2010, doi: 10.1021/ie100476q.
[4] K. H. G. Rätze, M. Jokiel, N. M. Kaiser, und K. Sundmacher, „Cyclic operation of a semi-batch reactor for the hydroformylation of long-chain olefins and integration in a continuous production process“, Chem. Eng. J., Bd. 377, S. 120453, Dez. 2019, doi: 10.1016/j.cej.2018.11.151.
[5] M. Jokiel u. a., „Miniplant-Scale Evaluation of a Semibatch-Continuous Tandem Reactor System for the Hydroformylation of Long-Chain Olefins“, Ind. Eng. Chem. Res., Bd. 58, Nr. 7, S. 2471–2480, Jan. 2019, doi: 10.1021/acs.iecr.8b03874.
[6] N. M. Kaiser, R. J. Flassig, und K. Sundmacher, „Reactor-network synthesis via flux profile analysis“, Chem. Eng. J., Bd. 335, S. 1018–1030, Sep. 2017, doi: 10.1016/j.cej.2017.09.051.
[7] N. M. Kaiser, R. J. Flassig, und K. Sundmacher, „Probabilistic reactor design in the framework of elementary process functions“, Comput. Chem. Eng., Bd. 94, S. 45–59, Nov. 2016, doi: 10.1016/j.compchemeng.2016.06.008.
[8] N. M. Kaiser, M. Jokiel, K. McBride, R. J. Flassig, und K. Sundmacher, „Optimal Reactor Design via Flux Profile Analysis for an Integrated Hydroformylation Process“, Ind. Eng. Chem. Res., Bd. 56, Nr. 40, S. 11507–11518, Sep. 2017, doi: 10.1021/acs.iecr.7b01939.
[9] N. M. Kaiser, „Dynamic optimization based reactor synthesis and design under uncertainty for liquid multiphase processes“, Ph.D. Thesis, Otto-von-Guericke-Universität, Magdeburg, 2019. [Online]. Verfügbar unter: 10.25673/25399
[10] G. Liesche, D. Schack, K. H. G. Rätze, und K. Sundmacher, „Thermodynamic Network Flow Approach for Chemical Process Synthesis“, in Computer Aided Chemical Engineering, Bd. 43, Elsevier, 2018, S. 881–886. doi: 10.1016/B978-0-444-64235-6.50154-6.
[11] G. Liesche, D. Schack, und K. Sundmacher, „The FluxMax approach for simultaneous process synthesis and heat integration: Production of hydrogen cyanide“, AIChE J., Bd. 65, Nr. 7, S. e16554, Juli 2019, doi: 10.1002/aic.16554.
[12] D. Schack, G. Liesche, und K. Sundmacher, „The FluxMax approach: Simultaneous flux optimization and heat integration by discretization of thermodynamic state space illustrated on methanol synthesis process“, Chem. Eng. Sci., Bd. 215, S. 115382, Apr. 2020, doi: 10.1016/j.ces.2019.115382.
[13] D. Schack, A. Jastram, G. Liesche, und K. Sundmacher, „Energy-Efficient Distillation Processes by Additional Heat Transfer Derived From the FluxMax Approach“, Front. Energy Res., Bd. 8, Juli 2020, doi: 10.3389/fenrg.2020.00134.
[14] D. Schack, Liesche, Georg, und Sundmacher, Kai, „Simultaneous Heat and Mass Flow Optimization of a Distillation Column Applying the FluxMax Approach“, Chem. Eng. Trans., Bd. 76, S. 337–342, Okt. 2019, doi: 10.3303/CET1976057.
