Boundary Feedback Stabilization Using Non-Conforming Finite Elements
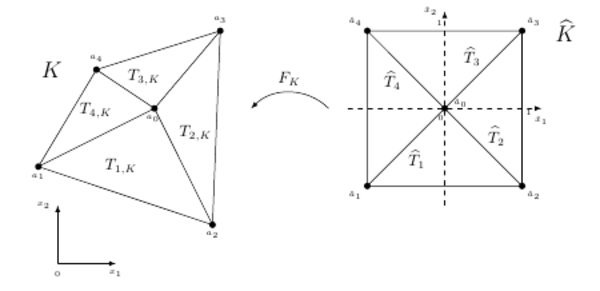
We are investigating a new finite element method to improve boundary feedback stabilization techniques of instationary, incompressible flow problems. Since standard finite elements do not fulfill divergence freeness condition by themselves we cannot guarantee the validity of this condition after solving the arising linear systems by iterative solvers. We, now, formulate the boundary feedback approach in operator terms and solve the underlying PDE in each step, where the divergence freeness condition is handled inside the solver. By using special finite elements we can improve the solver and end up with a fast robust algorithm.