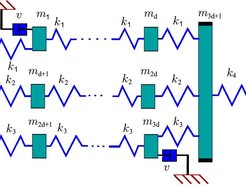
Optimal Damping of Vibrating Systems
In real physical systems which possess elasticity and mass, dangerous vibrations are a typical phenomenon which have been widely studied in the past. Up to this day it is an intensively investigated phenomenon. For the majority of engineering applications, resonance and sustained oscillations can cause structural damage. The way to reduce dangerous vibrations is through damping. Damping can also produce undesirable effects such as energy waste or heat production. On the other hand, damping is also responsible for many important system properties such as stability and dissipativity. Our investigation is devoted to optimization of damping of vibrating systems which is a very demanding problem.
Thus, our goal is to develop efficient approaches for solving problems which appear in damping optimization but also in closely connected issues such as optimality of the solution of the linear systems, stability via Lyapunov and optimal control. Another problem is the analysis of the system structure induced by the dissipativity of the system. Solving such problems is both a highly relevant and difficult task. We also investigate algorithms which can accelerate the optimization process while still ensuring accuracy.
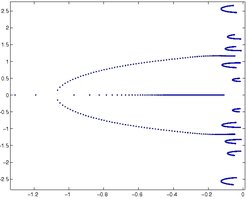
This project will deal with optimizing certain robustness measures in order to make the controlled system robust with respect to perturbations. Therefore, we consider ![]() norm optimization as well as feedback stabilization and eigenvalue assignment problems for large-scale and medium-sized dynamical systems. We will investigate the possibility of applying a new approach for robust control of such systems based on pseudospectra.
norm optimization as well as feedback stabilization and eigenvalue assignment problems for large-scale and medium-sized dynamical systems. We will investigate the possibility of applying a new approach for robust control of such systems based on pseudospectra.
Within the ![]() norm optimization of large-scale dynamical systems, we will also consider optimization of the trace of the solution of the corresponding parameter dependent Lyapunov equation. We will use a new linearized model without a simultaneous diagonalization of the component matrices. For this problem a better understanding of the properties of large-scale dynamical systems is required. The usage of model order reduction approaches is investigated for this task, such that important system characteristics can be drawn at a highly reduced numerical effort from a reduced order model. Additionally, we will derive a theory which will describe the geometry of the corresponding eigenspaces as well as the relative perturbation bounds for corresponding eigenvalues.
norm optimization of large-scale dynamical systems, we will also consider optimization of the trace of the solution of the corresponding parameter dependent Lyapunov equation. We will use a new linearized model without a simultaneous diagonalization of the component matrices. For this problem a better understanding of the properties of large-scale dynamical systems is required. The usage of model order reduction approaches is investigated for this task, such that important system characteristics can be drawn at a highly reduced numerical effort from a reduced order model. Additionally, we will derive a theory which will describe the geometry of the corresponding eigenspaces as well as the relative perturbation bounds for corresponding eigenvalues.
For the numerical solution of the occurring matrix equation within this optimization process, we use methods developed at the MPI Magdeburg, e.g., low-rank ADI type methods.
Regarding the feedback stabilization we will also consider the case of active damping with direct velocity feedback, since one can obtain almost the same second order system as with passive damping. In particular, the system: ![]() with output
with output ![]() and an active control
and an active control ![]() leads to
leads to ![]() . Since the system is almost the same as in the investigation of passive damping, we investigate if some of our existing results can also be applied in active damping.
. Since the system is almost the same as in the investigation of passive damping, we investigate if some of our existing results can also be applied in active damping.