Global Optimization of Integrated Multiphase Systems
Motivation
Optimal design of chemical processes often leads to mixed integer nonlinear optimization problems (MINLP). In practice, local or stochastic optimization methods are oftenapplied in order to solve them. However, such methods cannot guarantee that a global optimum will be achieved. To overcome this problem , in recent years powerful methods for deterministic global optimization have been developed based on convex relaxations, e.g. Baron [9], SCIP [1], or ANTIGONE [8]. However, the computational effort for solving even relatively simple problems from the engineering point of view can be tremendous. In this project our aim is to reduce the computational effort by suitable model (re)formulation, bound tightening and relaxation strategies. Physical insight is leading the way to efficient solution strategies.
Approach/Results
From the application side, the focus is on the development of novel chemical processes from renewable resources in integrated liquid multiphase systems. So far, the main focus of our research has been on the hydroformylation of long chain olefines using thermomorphic solvents. Suitable methods for global optimization have been developed for this type of chemical reactors, as illustrated in Figure 1 [3].

Figure 1: Deterministic global optimization of a novel hydroformylation process. Influence of model formulation, relaxation strategies and model approximation on computational effort.
Computational costs were reduced by orders of magnitude. Besides the reaction also separation processes play an important role for the efficient separation of the products and the recycling of excess reactants and auxiliaries. Among the separation processes, distillation columns have a large impact on flowsheet optimization. Using monotonic reformulations, tailormade bound tightening or surrogate models with iterative refinement, global optimization of distillation columns becomes for the first time feasible with moderate computational effort in the order of minutes up to a few hours depending on the specific process (number of components, ’difficulty’ of separation) [6, 7, 2]. It has been shown that even for ideal mixtures under certain conditions global optimization can improve the design significantly compared to traditional approaches [4]. Furthermore, global optimization has also been applied to other multistage separation processes including membrane separation, melt and solution crystallization, leading to novel insights (see Figure 2). Comprehensive optimization studies have been performed for binary separations with different feed compositions, different separation factors and different objective functions to gain the complete picture. It has been found that all of these processes share the common feature that, in particular for low numbers of required stages, traditional countercurrent cascades are suboptimal. The physical explanation is that the overall amount of processed material can be significantly reduced by generating as much product as possible in a first stage such that purity specifications are met after mixing with a small amount of highly purified product from other stages. Substantial improvements in total costs of up to 35 %, compared to classical countercurrent cascades, and some simple design rules were derived from the rigorous global optimization results [6, 5].
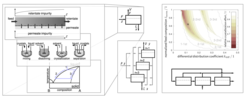
Figure 2: Global optimization of multistage separation process es involving melt and solution crystallization and membrane separation (left). Influence of network structure (middle) on process performance (right).
The project is embedded in the joint research center SFB/TR 63, funded by the DFG.
Cooperation Partners
- Project partners from TU Berlin and TU Dortmund
- PSE group
- PCF group
References
[1] Tobias Achterberg. Scip: solving constraint integer programs. Mathematical Programming Computation, 1(1):1–41, 2009.
[2] Tobias Keßler, Christian Kunde, Nick Mertens, Dennis Michaels, and Achim Kienle. Global optimization of distillation columns using surrogate models. SN Applied Sciences, 1(11), 2019.
[3] Tobias Keßler, Nick Mertens, Christian Kunde, Corina Nentwich, Dennis Michaels, Sebastian Engell, and Achim Kienle. Efficient global optimization of a novel hydroformylation process. Computer Aided Chemical Engineering, 40:2113–2118, 2017.
[4] Christian Kunde. Global Optimization in Conceptual Process Design. PhD thesis, Otto-von-Guericke University Magdeburg, 2017.
[5] Christian Kunde and Achim Kienle. Global optimization of multistage binary separation networks. Chemical Engineering and Processing - Process Intensification, 131:164– 177, 2018.
[6] Nick Mertens, Christian Kunde, Achim Kienle, and Dennis Michaels. A reformulation strategy for deterministic global optimization of ideal multi-component distillation processes. In Proceedings of the 26th European Symposium on Computer Aided Process Engineering, pages 691–696, 2016.
[7] Nick Mertens, Christian Kunde, Achim Kienle, and Dennis Michaels. Monotonic reformulation and bound tightening for global optimization of ideal multi-component distillation columns. Optimization and Engineering, 19(2):479–514, 2018.
[8] Ruth Misener and Christodoulos A. Floudas. Antigone: Algorithms for continuous integer global optimization of nonlinear equations. Journal of Global Optimization, 59:503–526, 2014.
[9] M. Tawarmalani and Nikolaos V. Sahinidis. A polyhedral branch-and-cut approach to global optimization. Mathematical Programming, 103(2):225–249, 2005.

