Model-based analysis of complex chromatographic processes
Equilibrium theory is a powerful tool for understanding, designing and controlling chromatographic processes. It is based on an idealized model, which neglects axial dispersion and assumes thermodynamic equilibrium between the fluid and the solid phase. It represents a system of first order quasilinear partial differential equations and admits an analytical approach using the method of characteristics. Thermodynamic equilibrium is described by the sorption isotherm, which represents the essential nonlinearity of the system. Previous approaches - including our own work (e.g. [R1-R3]) - have mostly been limited to explicit sorption isotherms including Langmuir, Bi-Langmuir and generalized Langmuir isotherms (see, e.g., [R4]).
The focus of this project has been on processes with implicit sorption isotherms which are often required for an accurate process description. A typical example is stoichiometric ion exchange. Our approach extends the classical results by Tondeur, Helfferich and Klein (see, e.g., [R5] and references therein) to full chromatographic cycles and pulse patterns. Further, it accounts for variable solution normalities and steric hindrance [1]. The latter plays an important role in the separation of larger molecules. On the basis of these theoretical results, a design method for ion exchange multicolumn simulated moving bed processes has been developed using triangle theory [2]. The results are illustrated in Fig. 1 on the left. In this figure, the triangle represents the region of total separation in the parameter plane of the flow rate ratios in zones 2 and 3. Also shown in Fig. 1 is an approximate triangle which is obtained if an explicit Langmuir isotherm is fitted to the implicit ion exchange sorption isotherm and the standard equations for Langmuir isotherms are used [R6]. Such an approach will lead to suboptimal or even infeasible solutions. Also, additional parameters, such as solution normality, which can influence process performance significantly, cannot be addressed explicitly by this simplified approach.
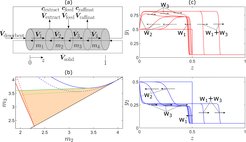
Recent attention was also given to the effect of finite mass transfer and finite axial dispersion. First, focus was on Langmuir isotherms and a single shock profile. For this case, an elegant analytical approach is available for equal mass transfer or dispersion coefficients [R7-R8]. An analytical treatment has not yet been found for different mass transfer coefficients and/or different dispersion coefficients . Alternatively, we proposed simple approximate solutions, which can be fitted online to the process and used for model-based control [3]. In a second step, we focused on Riemann problems with multiple shock profiles playing an important role in many countercurrent separation processes. It has been known for a long time that the pinch states of such profiles depend on the ratios of the mass transfer and/or dispersion coefficients [R9]. We have now analyzed this in more detail and it was shown that this surprising behavior can be explained by wave reflections at the system boundaries that have not been observed for the case of equal coefficients. An example is shown in Fig. 1 on the right, where wave w2 is reflected at the left boundary into wave w3 . In the future we want to use this knowledge for model reduction purposes using extended wave models.
Further research activities in this field in cooperation with the PCF group concern the design of multicomponent continuous separation processes with more than two components [4].
Cooperation partners
- Prof. Seidel-Morgenstern, PCF group
- Prof. Kaspereit, FAU Erlangen-Nuremberg
Publications
[1] M. Fechtner and A. Kienle. Equilibrium theory of ion exchange with variable solution normality and steric hindrance. Chem. Eng. Sci., 199:508–527, 2019.
[2] M. Fechtner and A. Kienle. Rational design of ion exchange simulated moving bed processes. In Computer Aided Chem. Eng., 48:733-738, 2020.
[3] M. Fechtner and A. Kienle. Approximate shock layer solutions for the separation of multicomponenet mixtures with different axial dispersion or mass transfer coefficients. Chem. Eng. Sci., 231:116335, 2021.
[4] J. W. Lee, A. Kienle, and A. Seidel-Morgenstern. Numerical short-cut design of simulated moving bed processes for multicomponent nonlinear adsorption isotherms: Nonstoichiometric langmuir isotherm, 2021. Ind. Eng. Chem. Res., 2021. DOI: 10.1021/acs.iecr.1c00671.
[R1] S. Grüner and A. Kienle. Equilibrium theory and nonlinear waves for reactive distillation columns and chromatographic reactors. Chem. Eng. Sci., 59:901–918, 2004.
[R2] M. Kaspereit, A. Seidel-Morgenstern, and A. Kienle. Design of simulated moving bed processes under reduced purity requirements. J. Chromatogr. A, 1162:2–13, 2007.
[R3] D. Flockerzi, M. Kaspereit, and A. Kienle. Spectral properties of Bi-Langmuir isotherms. Chem. Eng. Sci., 104:957–959, 2013.
[R4] M. Mazzotti and A. Rajendran. Equilibrium theory-based analysis of nonlinear waves in separation processes. Ann. Rev. Chem. Biomol. Eng., 4:119–141, 2013.
[R5] Friederich G. Helfferich and G. Klein. Multicomponent Chromatography. Theory of Interference. M. Dekker, New York, 1970.
[R6] C. Migliorini, M. Mazzotti, and M. Morbidelli. Continuous chromatographic separation through simulated moving beds under linear and nonlinear conditions. J. Chromatogr. A, 827:161–173, 1998.
[R7] Hyun-Ku Rhee, Rutherford Aris, and Neal R. Amundson. First-Order Partial Differential Equations: Volume II – Theory and Application of Hyperbolic Systems of Quasilinear Equations. Prentice Hall, New Jersey, 1989.
[R8] M. Mazzotti, G. Storti, and M. Morbidelli. Shock layer analysis in multicomponent chromatography and countercurrent adsorption. Chem. Eng. Sci., 49:1337–1355, 1994.
[R9] S. Sundaresan, J. K. Wong, and R. Jackson. Limitations of the equilibrium theory of countercurrent devices. AIChE J., 33:1466–1472, 1987.
