Mixed Integer Nonlinear Programming for Damping Optimization
Vibrations are a typical and a mostly unwanted phenomenon in mechanical systems. Resonance and sustained oscillations have undesired effects such as energy waste, noise creation and even structural damage. The way to reduce dangerous vibrations is through damping. Damping is also responsible for many important system properties such as stability and dissipativity. Our investigation is devoted to damping optimization.
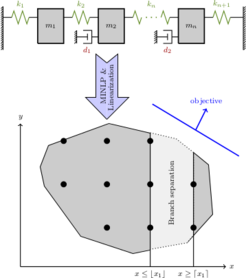
The problem we will consider is to determine dampers' position and viscosities for a vibrational system. A criterion in the optimization problem is to minimize the total energy for a vibrational system over all initial states of unit energy, and all dampers' positions and its viscosities. In general this is a Mixed Integer Nonlinear Program (MINLP) as viscosities represent real numbers, while positions are given as coordinates in the network, indexed by nonnegative integers.
Various approaches have been investigated: discrete to continuous approaches (e.g., by using Nelder-Mead methods) and/or some discretization of the dampers' and viscosity space and solving the Lyapunov matrix equation for the dampers' position and viscosities. But the main drawback is the combinatorial explosion of the total number of damping combinations. Therefore, we would like to use recent advances in MINLP.
Furthermore, we would like to address the linearization of the MINLP, which in this case is possible since the product of variables can be expressed as separable functions. Hence, we end up with an Integer Program (IP). In this context we will discuss branching strategies, branch-and-bound, branch-and-cut, pricing and heuristics to overcome the combinatorial explosion. In this setting, we would like to discuss and compare the results from the MINLP and IP approaches with the previously investigated and abovely mentioned discrete to continuous approaches.
Furthermore, we would like to consider a new damping optimization problem when a mechanical system is excited by an external force. In this case we consider a new criterion which is based on the amplitude, such as average energy amplitude and average displacement amplitude criterion.
With the knowledge of damping based on total energy we will derive explicit formulas for particular case studies. In the general setting we will propose approaches in which the objective function can be efficiently calculated. Moreover, in this optimization problem we would like to employ MINLP as well in order to determine optimal damping efficiently.