Adaptively Synthesized Surrogates for Reliable and Efficient Model Order Reduction

This project focuses on advanced model order reduction (MOR) algorithms for parametric nonlinear dynamical systems. We propose efficient error estimators by taking use of machine learning; we apply our proposed adaptive sampling techniques and error estimation to real-world problems, including cardiac models; we propose tensor-based sparse sampling techniques which are accurate for efficient sensor placement and fast hyper-reduction; we propose cheap and effective error estimators for parametric linear and nonlinear systems.

Reliable ROMs through ML-enhanced closure modeling

Projection-based model reduction methods have been widely adopted for speeding up simulations of large-scale dynamical systems in numerous engineering applications [1]. The reduced basis method (RBM) has found particular success owing to its efficiency and error certification [2,3]. For the RBM applied to dynamical systems, the POD-Greedy algorithm is the preferred approach, known for its efficiency and well-established convergence properties [4]. Despite the many attractive properties of the RBM, a key disadvantage it encounters is the need to have full knowledge about the time integration scheme used to solve a dynamical system whose reduced model is sought. This limits the usage of RBM in applications where adaptive time-stepping and adaptive order schemes are used. Such solvers are routinely found in libraries such as PETSc, SUNDIALS and also in scientific computing software, e.g., MATLAB (ode45, ode15s, etc.) and Python (scipy.integrate.odeint) which are commonly used in engineering simulations. In this project, we address this limitation of the RBM by developing a data-enhanced closure modelling framework [5].

The part of the RBM that requires knowledge about the time integration scheme is the a posteriori error estimator. We develop a new a posteriori error estimator for nonlinear dynamical systems which is independent of the choice of the time integration method. In our framework, a user-defined time integration scheme (of any desired order) is first imposed on the full-order model (FOM). This is referred to as the corrected FOM (or C-FOM). The C-FOM has a data-driven closure term which accounts for any mismatch that arises between the solution of the true FOM and that of the C-FOM. We follow standard Galerkin projection to obtain a corrected reduced-order model (C-ROM) from the C-FOM. The main idea is that this C-ROM can be time integrated using the user-defined method and the resulting time evolution will closely match the one obtained by evolving the true ROM, provided the closure-term is accurate. This implies that the C-ROM can be used to evaluate the residual-based a posteriori error estimator as in the standard RBM framework, circumventing any lack of knowledge about the time integration method. We develop and prove a rigorous a posteriori error bound for the output error. A computable relaxation of this upper bound in the form of an error estimator is also developed.

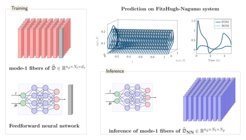
The success of the C-ROM based error estimator relies on how well the closure term is approximated. We conjecture certain low-rank and smoothness properties for the snapshots of the closure term and demonstrate it numerically. These properties are then leveraged to obtain a computationally efficient scheme to approximate the closure term. Two different approaches based on radial-basis interpolation and deep feed-forward neural network approximation are developed and numerically validated. The overall ML-enhanced closure modelling framework for a posteriori error estimation is tested on three large-scale numerical examples from different fields such as fluid dynamics (Burgers' equation), neuron modelling (FitzHugh-Nagumo equations), and process engineering (batch chromatography). The proposed framework leads to robust ROMs that are efficient and generalize very well.

 

Fast and reliable ROMs for cardiac electrophysiology (in collaboration with TU Dresden)

Repeated evaluations of high-dimensional discretized systems is often needed in the context of applications like parameter estimation, uncertainty quantification, and control. To enable this in a computationally efficient manner, model order reduction (MOR) techniques have been developed and studied over the last five decades [1]. Cardiac modelling is a recent application area for MOR techniques [6] where reduced-order models (ROMs) are often necessary to overcome the computational challenges posed by the high complexity of the human heart, viz., high-dimensionality, nonlinearity, strong coupling between different physics. While established MOR techniques like the proper orthogonal decomposition (POD) and the discrete empirical interpolation method (DEIM) [7] have been applied for cardiac ROMs recently, these approaches are often heuristic and lack reliability. Reliability of the ROMs and their ability to generalize well is particularly relevant for high-consequence applications like cardiac modeling.

 

This project builds on prior work in our group on adaptive MOR [8,9] and utilizes that framework to develop ROMs for cardiac electrophysiology [10]. Cardiac electrophysics is modelled as a system of two coupled partial differential equations, adopting the Aliev-Panfilov model which couples the trans-membrane potential within the domain and the recovery voltage. We extend the adaptive model reduction framework to deal with coupled systems and develop an a posteriori output error estimator for the ROM. This error estimator is subsequently used within an iterative procedure that adaptively updates the projection basis and the parameter training set. A bi-fidelity interpolation scheme based on radial basis functions is developed to address the high computational cost of having many samples in the parameter training set. Two benchmark examples are used to exemplify the benefits of using the adaptive MOR framework for cardiac ROMs. One advantage of this is that the ROMs are certified, meaning the user can trust them for downstream applications mentioned previously, such as uncertainty quantification. An additional benefit of adaptivity is that it greatly reduces the training cost for MOR.

So far, we considered adaptive MOR in a linear projection setting. This can be a limitation whenever the system being modelled exhibits strong wave-like behaviour. One of the examples we considered [6] belongs in this category. To well-approximate such dynamics, the ROM dimension needs to be very large. Currently, we are exploring nonlinear/manifold projections within the adaptive MOR framework to obtain small ROMs.

 

Leveraging tensor representations for sparse function approximation

The approximation of parametrized functions from sparsely measure data is relevant in numerous application such as model order reduction, sensor placement, and feature selection. Existing approaches to address this problem, especially in the model order reduction context, include the empirical interpolation method [11] and its special case, the discrete empirical interpolation method [12]. A major drawback of these methods is that they matricize the snapshots data. When the underlying data has a natural tensor structure, e.g., data from the discretization of partial differential equations, matricization leads to the loss of the geometric structure, potentially leading to poor approximation.

We develop a new framework for sparse function approximation of 3-D data called the tensor t-product Q-DEIM (t-Q-DEIM) [13], extending the Q-DEIM approach [14]. This framework leverages the tensor t-product representation [15] to retain the natural tensor structure, avoiding the smearing out of any correlations between the different dimensions caused by matricization. We make use of the t-product singular value decomposition (t-SVD) to obtain a suitable tensor-valued basis for the approximation of the tensor data. Furthermore, for identifying the sparse interpolation points, the pivoted t-product QR decomposition (t-pQR) [16] is leveraged. As the central theoretical contribution, we develop a rigorous, computable error bound for the error between the true data and its t-product Q-DEIM-based approximation. An a-priori estimate for one of the terms involved in our error bound is also proposed. Examples from five diverse applications are used to illustrate the improved approximation quality and better computational efficiency of the t-Q-DEIM framework over the state-of-the-art.

 

Inf-sup-constant-free error estimators for model order reduction of parametric systems (in collaboration with the Polytechnic University of Madrid (UPM))

A posteriori error estimation is critical for ensuring the reliability of reduced-order models (ROMs). Such error estimators constitute a crucial part of model reduction techniques such as the reduced basis method (RBM) [2] where they are used in guiding the greedy choice of parameter samples. This calls for error estimators that are able to provide a sharp estimate for the underlying true error incurred by ROMs. A widely noted drawback associated with existing residual-based error estimators is their lack of robustness for problems where a quantity called the inf-sup-constant is small. Such problems are often found in computational electromagnetics, especially for systems which exhibit resonance behaviour. The retention of the (small magnitude) inf-sup-constant in the denominator of existing error estimators means that the estimated error can be unrealistically large.

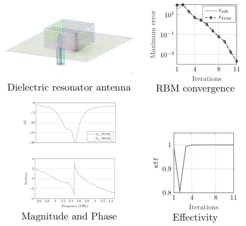
To address the above challenge, in this project we developed inf-sup-constant-free a posteriori error estimators. In the first stage, we developed such an error estimator for linear parametric systems [17]. We develop a framework that uses the relationship between the error and the residual. In this approach, a ROM for this error-residual system is constructed and its solution is then used to directly approximate the error in a low-dimensional subspace. This avoids the need to compute the inf-sup-constant and paves the way for both efficient and sharp error estimation. The developed framework is tested on several large-scale examples arising from microwave and antenna circuits used in communication applications.

As an extension of the above framework, we also developed similar inf-sup-constant-free error estimators for parametric nonlinear dynamical systems [18]. The extension specifically targets the error in the output quantity of interest and is based on the error estimator developed in [8]. We develop a dual system and its ROM, for the model being considered. For this dual pair, we synthesize a corresponding (dual) error-residual system and identify its ROM. Solving the ROM of this (dual) error residual system allows for the direct evaluation of the error, avoiding the need to compute the inf-sup-constant. To ensure computational efficiency, we propose the simultaneous greedy construction of the two bases for the dual systems. We illustrate the superior aspects of the new inf-sup-free error estimator by using it within the RBM. Two example, the 2-D Burgers’ equation and the FitzHugh-Nagumo equations are considered. Using the inf-sup-constant-free error estimator leads to a significant reduction in the offline time needed for basis construction, without losing any accuracy compared to the standard RBM.

 

References:

[1] Peter Benner, Serkan Gugercin, Karen Willcox, A survey of projection-based model reduction methods for parametric dynamical systems, SIAM Review, vol. 57, no. 4, pp. 483–531, 2015

[2] Alfio Quarteroni, Andrea Manzoni, Federico Negri,  Reduced Basis Methods for Partial Differential Equations An Introduction, Unitext La Matematica per il 3+2, 92, Springer, Cham, 2016

[3] Mario Ohlberger, Stephan Rave, Reduced basis methods: success, limitations and future challenges, In Proceedings of the Conference Algoritmy, pp. 1--12, 2016

[4] Bernard Haasdonk, Convergence rates of the POD-Greedy method, ESAIM: Mathematical Modelling and Numerical Analysis, vol. 47, no. 3, pp. 859--873, 2013

[5] Sridhar Chellappa, Lihong Feng, Peter Benner, Accurate error estimation for model reduction of nonlinear dynamical systems via data-enhanced error closure, Computer Methods in Applied Mechanics and Engineering, vol. 420, no. 116712, pp. 1--29, 2024

[6] Andrea Manzoni, Diana Bonomi, Alfio Quarteroni, Reduced order modeling for cardiac electrophysiology and mechanics: new methodologies, challenges and perspectives, In: Mathematical and Numerical Modeling of the Cardiovascular System and Applications, pp. 115--166, SEMA SIMAI Springer Series, Springer, Cham, 2018

[7] Diana Bonomi, Andrea Manzoni, Alfio Quarteroni, A matrix DEIM technique for model reduction of nonlinear parametrized problems in cardiac mechanics, Computer Methods in Applied Mechanics and Engineering, vol. 324, pp. 300--326, 2017

[8] Sridhar Chellappa, Lihong Feng, Peter Benner, Adaptive basis construction and improved error estimation for parametric nonlinear dynamical systems, International Journal for Numerical Methods in Engineering, vol. 121, no. 23, pp. 5320–5349, 2020

[9] Sridhar Chellappa, A Posteriori Error Estimation and Adaptivity for Model Order Reduction of Large-Scale Systems (Ph.D. thesis), Otto-von-Guericke-Universität, Magdeburg, Germany, 2022

[10] Sridhar Chellappa, Baris Cansız, Lihong Feng, Peter Benner, Michael Kaliske, Fast and reliable reduced-order models for cardiac electrophysiology, GAMM-Mitteilungen, vol. 46, eID: e202370014, 2023

[11] Maxime Barrault, Yvon Maday, Ngoc Cuong Nguyen, and Anthony T. Patera, An ‘empirical interpolation’ method: application to efficient reduced-basis discretization of partial differential equations, Comptes Rendus Mathematique Paris, vol. 339, no. 9, pp. 667-672, 2004

[12] Saifon Chaturantabut and Danny C. Sorensen, Nonlinear model reduction via discrete empirical interpolation, SIAM Journal on Scientific Computing, vol. 32, no. 5, pp. 2737–2764, 2010

[13] Sridhar Chellappa, Lihong Feng, Peter Benner, Discrete empirical interpolation in the tensor t-product framework, e-print 2410.14519, arXiv, math.NA, 2024

[14] Zlatko Drmac, Serkan Gugercin, A new selection operator for the discrete empirical interpolation method — improved a priori error bound and extensions, SIAM Journal on Scientific Computing, vol. 38, no. 2, pp. A631–A648, 2016

[15] Misha E. Kilmer, Carla D. Martin, Factorization strategies for third-order tensors, Linear Algebra and its Applications, vol. 435, no. 3, pp. 641–658, 2011

[16] Ning Hao, Misha E. Kilmer, Karen Braman, Randy C. Hoover, Facial recognition using tensor-tensor decompositions, SIAM Journal on Imaging Sciences, vol. 6, no. 1, pp. 437–463, 2013

[17] Sridhar Chellappa, Lihong Feng, Valentin de la Rubia, P. Benner, Inf-Sup-Constant-free state error estimator for model order reduction of parametric systems in electromagnetics, IEEE Transactions on Microwave Theory and Techniques, vol. 71, no. 11, pp. 4762-4777, 2023

[18] Lihong Feng, Sridhar Chellappa, Peter Benner, A posteriori error estimation for model order reduction of parametric systems, Advanced Modeling and Simulation in Engineering Sciences, vol. 11, no. 5, pp. 1–34, 2024