Non-intrusive Surrogate Modelling

This project aims to advance parametric non-intrusive surrogate modeling by developing innovative techniques. Our proposed approaches include: Kernel-based shallow neural networks (KSNNs) with a novel training procedure to rapidly construct accurate interpolants/regressors; POD-KSNN surrogate model that performs a parameter-specific proper orthogonal decomposition (POD) and strategically uses two KSNNs for efficient and accurate solution approximations; Error-estimator-enabled active learning (EEE-AL) and subspace-distance-enabled active learning (SDE-AL) frameworks to accelerate the offline surrogate construction using effective parameter sampling; Data-driven manifold learning via an improved kernel proper orthogonal decomposition strategy for effective surrogate modeling of convection-dominated problems; Tensor-based sparse sampling methods for optimal sensor placement, hyper-reduction, and active learning; Multi-stage tensor reduction framework for efficient and accurate surrogate modeling of systems presenting arbitrary order-p tensor-valued data. We test our approaches on complex systems, including challenging fluid flow problems featuring mixed convective and diffusive phenomena, multiple interacting shock profiles in the spatial domain, and flow scenarios exhibiting Hopf bifurcation across the parameter domain.

KSNN and POD-KSNN surrogate

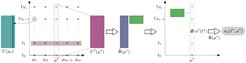
The proposed KSNN [1] is equipped with kernel activation functions, where the kernel widths and their center locations are adaptive, allowing the creation of accurate interpolants/regressors. Furthermore, employing our novel alternating dual-staged iterative training procedure [1] provides a fast construction of the shallow neural network. Figure 1 illustrates the approximation for two functions and shows the learned kernel widths and center locations. The POD-KSNN surrogate [1] approximates the solution in parameter-specific POD subspaces. Figure 2 provides a schematic overview of the approach. It builds a KSNN in the offline and the online phases, decoupling the interpolation/regression tasks between the parameter and time domains. The surrogate features fast offline construction and online query, offering a speedup of several orders of magnitude compared to the full-order model evaluations.

Figure 1. KSNN regression for two functions: the left column compares the KSNN prediction with the true values, and the right column shows the trained kernels and their center locations.

Figure 1. KSNN regression for two functions: the left column compares the KSNN prediction with the true values, and the right column shows the trained kernels and their center locations.

Figure 2. Framework for the POD-KSNN surrogate model.

Figure 2. Framework for the POD-KSNN surrogate model.

Error-estimator-enabled active learning

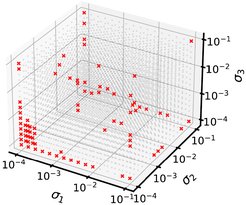
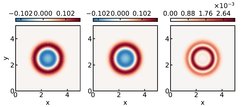
We provide a non-intrusive error-estimator-based optimality criterion to efficiently populate the parameter snapshots, thereby enabling the effective construction of parametric non-intrusive surrogates. The proposed EEE-AL framework [1] actively builds surrogates that meet a user-specified prediction error tolerance, displaying an efficient training set adaptivity and parameter-specific POD subspace adaptivity. Moreover, the framework is augmented to treat noisy data. The final parameter set and the solution predictions at test locations for the parametric thermal block problem are shown in Figures 3 and 4, respectively.

Figure 3. Parameter selection for the thermal block problem.

Figure 3. Parameter selection for the thermal block problem.

Figure 4. Solution approximation (top) and its error (bottom) for the thermal block problem at a test time instance and two test parameter samples.

Figure 4. Solution approximation (top) and its error (bottom) for the thermal block problem at a test time instance and two test parameter samples.

Subspace-distance-enabled active learning

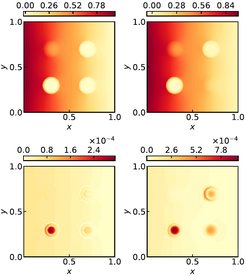
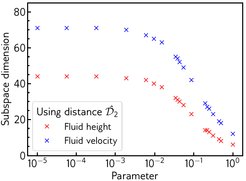
The SDE-AL procedure drives the selection of critical parameter locations during the offline stage by comparing the distance between parameter-specific linear subspaces. To accomplish this, we propose a new distance measure that evaluates the similarity between subspaces of different sizes. Due to the distance measure being computationally cheap, it facilitates repeated distance evaluations between numerous subspace pairs efficiently, thereby enabling a fast parameter sampling mechanism. The developed framework is flexible and applicable to any surrogate modeling technique. We particularly showcase the application of the SDE-AL framework over the POD-KSNN [1] and POD-NN [2] surrogates, proposing their efficient active-learning-driven counterparts. The final parameter set and the fluid height predictions at test parameter samples for a parametric flow governed by the shallow water equations are shown in Figures 5 and 6, respectively.

Figure 5. Parameter selection and the corresponding subspace dimension for the shallow water equations.

Figure 5. Parameter selection and the corresponding subspace dimension for the shallow water equations.

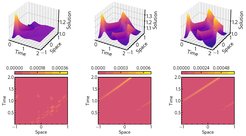
Figure 6. Fluid height predictions (top) and its error (bottom) at test parameter samples and test time instances for a parametric flow governed by the shallow water equations.

Figure 6. Fluid height predictions (top) and its error (bottom) at test parameter samples and test time instances for a parametric flow governed by the shallow water equations.

Data-driven manifold learning

Figure 7. Solution approximation (middle), its error (right), and the true solution (left) for the hyperbolic wave equation at a test parameter sample and test time instance.

Figure 7. Solution approximation (middle), its error (right), and the true solution (left) for the hyperbolic wave equation at a test parameter sample and test time instance.

A crucial component of any surrogate model is the employed dimensionality reduction procedure. Traditionally, POD has been utilized in various surrogate modeling approaches. However, POD is limited to providing linear compression, which is restrictive for problems with complex nonlinear phenomena, especially those exhibiting slow Kolmogorov N-width decay. To address this limitation, nonlinear dimensionality reduction techniques based on deep learning, such as various autoencoder architectures---fully connected, convolutional, or graph-based---have been employed, which can learn an accurate low-dimensional manifold. However, these methods are computationally intensive. We propose a manifold learning framework by using kernel POD [3]. Herein, we improve upon the state-of-the-art forward and backward mappings to enhance the reduction procedure, focusing on efficient and effective compression from both informational and computational standpoints. Figure 7 shows the solution approximation for the hyperbolic wave equation at a test location.

Tensor-based sparse sampling

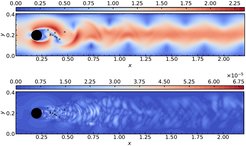
Figure 8. Solution reconstruction (top) and its error (bottom) using the sparse measurements (crosses) at a test sample of the Reynolds number for a high-dimensional parametric fluid flow problem governed by the incompressible Navier-Stokes equations.

Figure 8. Solution reconstruction (top) and its error (bottom) using the sparse measurements (crosses) at a test sample of the Reynolds number for a high-dimensional parametric fluid flow problem governed by the incompressible Navier-Stokes equations.

We propose tensor variants for the (discrete) empirical interpolation method using the tensor t-product framework [4]. In comparison with their matrix counterparts---EIM [5], DEIM [6], and Q-DEIM [7]---all our proposed variants show a significant improvement in reconstructing tensor-valued datasets from optimally-located sparse sensor measurements. This results from retaining the native tensor structure of the underlying dataset instead of matricizing it. Figure 8 shows the excellent solution reconstruction at an illustrative test location for a high-dimensional parametric fluid flow problem governed by the incompressible Navier-Stokes equations.

Multi-stage tensor reduction

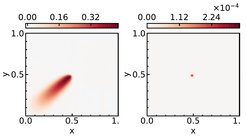
Figure 9. Solution approximation (left) and its error (right) for the Burgers’ equation with an order-4 solution tensor at a test sample of the viscosity.

Figure 9. Solution approximation (left) and its error (right) for the Burgers’ equation with an order-4 solution tensor at a test sample of the viscosity.

We propose a novel multi-stage tensor reduction (MSTR) framework for tensorial data arising from experimental measurements or high-fidelity simulations of physical systems using the tensor t-product framework [4]. The order p of the tensor under consideration can be arbitrarily large. At the heart of the framework are a series of strategic tensor factorizations and compressions, ultimately leading to a final order-preserving reduced representation of the original tensor. We also augment the MSTR framework by performing efficient kernel-based interpolation/regression over certain reduced tensor representations, amounting to a new non-intrusive surrogate modeling approach capable of handling dynamical, parametric steady, and parametric dynamical systems. Furthermore, to efficiently build the parametric surrogate in the offline stage, we employ our tensor-based sparse sampling methods to select important parameter locations for the full-order model evaluation. Figure 9 provides a solution approximation for the Burgers’ equation with an order-4 solution tensor at a test location.

References

[1] H. Kapadia, L. Feng, and P. Benner. Active-learning-driven surrogate modeling for efficient simulation of parametric nonlinear systems. Computer Methods in Applied Mechanics and Engineering, 419:1–36, No. 116657, 2024.

[2] Q. Wang, J. S. Hesthaven, and D. Ray. Non-intrusive reduced order modeling of unsteady flows using artificial neural networks with application to a combustion problem. Journal of Computational Physics, 384:289–307, 2019.

[3] M. Salvador, L. Dedè, and A. Manzoni. Non intrusive reduced order modeling of parametrized PDEs by kernel POD and neural networks. Computers & Mathematics with Applications, 104:1–13, 2021.

[4] M. E. Kilmer and C. D. Martin. Factorization strategies for third-order tensors. Linear Algebra and its Application, 435(3):641–658, 2011. Special issue: Dedication to Pete Stewart on the occasion of his 70th birthday.

[5] M. Barrault, Y. Maday, N. C. Nguyen, and A. T. Patera. An ‘empirical interpolation’ method: application to efficient reduced-basis discretization of partial differential equations. Comptes Rendus Mathematique, 339(9):667–672, 2004.

[6] S. Chaturantabut and D. C. Sorensen. Nonlinear model reduction via discrete empirical interpolation. SIAM Journal on Scientific Computing, 32(5):2737–2764, 2010.

[7] Z. Drmač and S. Gugercin. A new selection operator for the discrete empirical interpolation method—improved a priori error bound and extensions. SIAM Journal on Scientific Computing, 38(2):A631–A648, 2016.