Data-Driven System Reduction and Identification  

• Prof. Antoulas is renowned for his fundamental research contributions
• This Festschrift is being published for a conference to celebrate Antoulas's 70th birthday
• Model reduction is a timely and important area with many scientific and engineering applications.

more

Successfully commercializing polymer electrolyte membrane fuel cells (PEMFC) requires their durability to be improved. In order to achieve this goal, many studies have been devoted to developing diagnostic methodologies for the early detection of material degradation symptoms, identifying the causes of degradation mechanisms, and developing mitigation strategies to extend the lifetime of these devices. The application of the Loewner framework for analyzing the input-output data of PEMFCs facilitates the interpretation of the related frequency domain spectra and significantly reduces the time needed for performing the frequency response experiments. In particular, based on the transfer functions resulting from data, it was possible to calculate the characteristic frequencies (DCF), which enable the identification of the polarization losses related to all the phenomena underlying the EIS spectra. Additionally, incorporating the Loewner framework in the analysis of cFRA data allows time reduction of experiments up to 60%. Hence the application of this methodology as an online diagnostic tool in mobile applications becomes feasible. Joint research between the two groups (DRI and EEC) is currently underway.

One challenge that arises in the development of interpolation-based rational approximation data-driven methods is the ability to enforce error bounds and conditions for optimality. Another challenge is approximating functions with discontinuities. In this direction, the Loewner framework has been applied to approximating the sign function. For this particular test case, the optimal solution is known from the work of the Russian mathematician, E. I. Zolotarev. Another example is the absolute value function, which is a continuous function, non-differentiable at the origin. Approximating this function by polynomials played a significant role in the early development of approximation theory. We propose an extensive numerical study of approximating the absolute value function. The methods reviewed have been proposed relatively recently, for example, the Loewner framework, the AAA and Minimax algorithms (iterative methods). The result presented by D. J. Newman is at the heart of this study. more

Extensions of the Loewner Data-Driven Control (L-DDC) methodology are addressed. First, this approach is extended by incorporating two alternative approximation methods known as Adaptive-Antoulas-Anderson (AAA) and Vector Fitting (VF). These algorithms also include least-squares fitting which provides additional flexibility and enables possible adjustments for control tuning. Secondly, the standard model reference data-driven setting is extended to handle noise affecting the data and uncertainty in the closed-loop objective function. These proposed adaptations yield a more robust data-driven control design.  more

In applications, the effect of perturbations (such as noise in the measured data) must be analyzed. First, a factorization of the Loewner matrix pencil involved in data-driven modeling is explored. The first consequence is that the associated quadruple constructed from the data yields a model without requiring further processing. The second consequence is related to how sensitive the eigenvalues of the Loewner pencil are to perturbations. Based on explicit generalized eigenvalue decomposition of this pencil and by making use of perturbation theory of matrix pencils, we explore two types of eigenvalue sensitivities. The first one is defined with respect to unstructured perturbations of the Loewner pencil, while the second is defined for structured perturbations. The effect of the choice of data on the two sensitivities is also analyzed. Hence, this serves as a basis for selecting appropriate data sets. more

Another data-driven method that has emerged in recent years is the so-called operator inference framework (or OpInf). This approach uses time-domain state measurements (snapshots of the state variable), and then fits a particular nonlinear model (quadratic or quadratic-bilinear) by computing the appropriate matrices. This is done using least-squares type methods. One aspect that distinguishes the OpInf framework from the extended Loewner-based frameworks that we propose, is that the former requires measurements of the whole state variable. The latter framework requires only input-output measurements (transfer function measurements of higher-order generalized transfer functions). In this direction, we have pursued hybrid extensions of operator inference combined with the Loewner philosophy, in order to enforce approximation of the input-to-output mappings. For the book press: more

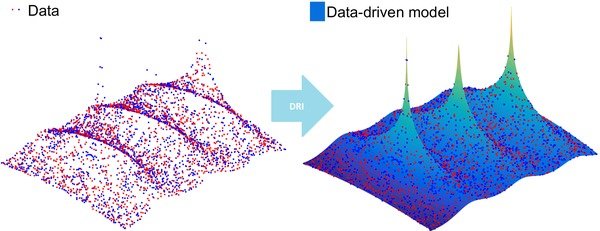
Machine Learning (ML) techniques have aimed to "learn" the black box. For specific tasks such as pattern recognition, ML has demonstrated remarkable success. The limitations of ML methods begin when the interpretation of the derived models is under consideration. By combining learning from data, with reduction techniques, we have introduced an approach that yields identification of reduced models from data (discovery of dynamical systems). It constitutes a non-intrusive method that deals with real data (engineering measurements such as frequency, velocity, current, and concentration) able to identify linear and nonlinear systems, and at the same time offer the opportunity for reduction that is crucial for simulation, design, and control.

The motivation behind considering the reduction of quadratic bilinear (QB) systems, is that the dynamics of many classical nonlinear PDEs can be expressed in terms of such nonlinearities without any approximation error. Examples include the Chafee-Infante, FitzHugh-Nagumo, Burgers', Stokes or Navier-Stokes equations. For the book press: more

Hybrid systems are a class of nonlinear systems which result from the interaction of continuous time dynamical subsystems with discrete events. Switched systems constitute a subclass of hybrid systems, in the sense that the discrete dynamics is simplified. A switched system is a dynamical system that consists of a finite number of subsystems and a logical rule that orchestrates switching between these subsystems. The motivation behind the study of hybrid and switched systems stems from the fact that they represent useful models for the design of distributed embedded systems where discrete controls are applied to continuous processes. more

In collaboration with researchers from the Baylor College of Medicine in Houston, the issue of oscillations in (mouse) genes was studied. The problem can be regarded as data-driven modeling where the data is given in the time-domain. The mathematical insights provided by the so-called pencil method led to new biological insights. In particular, it was shown that several genes exhibit 12h oscillations (in addition to 24h oscillations) and these two sets of oscillations turn out to be independent from each other. This leads to questions regarding the significance of the disruption of such oscillations for human disease. Access to the paper press: more

The Loewner framework has also been applied to approximating non-rational functions that arise from linear PDEs, e.g., describing a vibrating beam. Additionally, the approximation quality of the proposed method has been compared with other approximation methods such as the AAA (Adaptive-Antoulas-Anderson) algorithm, vector fitting or IRKA ( Iterative Rational Krylov Algorithm). The goal is to devise and improve methods that best exploit the information provided by data (measurements). This can be used to describe the above embedded minimal information in an efficient way, making use of the data-driven Loewner framework. For the book press: more

1. Connections between the Loewner framework and the behavioral approach of systems and control.
2. A posteriori error bounds in reduced-order modeling for which the main tool is the use of the dual system.
3. Addressing issues such as transfer functions of rectangular systems, stability, and DAE structure preservation.
4. Research toward discovering how worms implement control mechanism. For access to the presentation press: more