Adaptive MOR for parametric nonlinear systems

In the context of many-query scenarios in fields of design, optimization occurence of large-scale parameteric models is inevitable. Model reduction of parametric systems has received considerable attention in recent years. Here, we focus attention on nonlinear dynamical systems. With the help of error estimators and the powerful notion of adaptivity, it is possible to generate reduced order models (ROM) that are compact and amenable to repeated simulations, in a computationally cheap way.

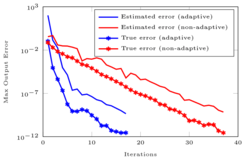
Proper orthogonal decomposition (POD) method combined with discrete empirical interpolation method (DEIM) [1] is one of the popular methods for model order reduction of general nonlinear systems. Usually, the number of POD basis and the number of DEIM basis are manually decided upon the decay of the singular values of the snapshot matrices of the solution and the nonlinear function, respectively. The number of both bases are conservatively kept large, in order to get a sufficiently accurate model. We aim to develop an approach that can adaptively update the number of both bases, and automatically derive a suitable match of the two bases by employing an efficient a posteriori output error estimation of the reduced-order model [2]. The error-estimator uses a primal-dual method to provide good effectivity. At each iteration, the number of POD modes to be updated is decided based on the logarithm of the ratio of the current POD error to the required error tolerance. The same approach is also adopted to update the DEIM basis.

The same idea can be extended to parametric systems. For this, we make use of the reduced basis approach [3]. The POD-GREEDY algorithm [4], selects parameters in a greedy fashion, from a user-defined training set. Data compression over the time variable is achieved using POD of the snapshots of the solution at the chosen greedy parameter. The solution of the dual system in the parametric case is done efficiently using the multi-moment matching method [5].

Our work focusses on,

- the automatic generation of ROMs through the idea of adaptivity that seeks an optimal balance of the number of POD and DEIM basis,

- developing improved and computationally efficient output error estimators (or bounds),

- adaptively choosing the parameters, snapshots.

The image compares the convergence of the output error (estimated vs. true), when using the adaptivity scheme on the POD-GREEDY algorithm and when not using it. The example shown is that of a parametric, viscous Burgers' equation.

The image compares the convergence of the output error (estimated vs. true), when using the adaptivity scheme on the POD-GREEDY algorithm and when not using it. The example shown is that of a parametric, viscous Burgers' equation.

References

[1]. S. Chaturantabut and D. C. Sorensen

Nonlinear model reduction via discrete empirical interpolation

SIAM Journal on Scientific Computing, 32 (5): 2737-2764, 2010.

Source

DOI

[2]. Y. Zhang, L. Feng, S. Li, and P. Benner

An efficient output error estimation for model order reduction of parametrized evolution equations

SIAM Journal on Scientific Computing 2015 37:6, B910-B936, 2015.

Source

DOI

[3]. A. Quarteroni, A. Manzoni, F. Negri

Reduced Basis Methods for Partial Differential Equations

UNITEXT - La Matematica per il 3+2, Springer, 2016

DOI

[4]. Bernard Haasdonk and Mario Ohlberger

Reduced Basis Method for finite volume approximations of parametrized linear evolution equations

ESAIM: M2AN, 42 2 (2008) 277-302.

Source

DOI

[5]. L. Feng, P. Benner

A robust algorithm for parametric model order reduction based on implicit moment matching

Reduced Order Methods for modeling and computational reduction, MS&A Series, volume 9, chapter 6 pages 159-186. Springer, Berlin, Heidelberg, New York, 2014.

Source

DOI