MOR for nonlinear model design of catalytic reactors
The current development in modern reaction engineering towards detailed multi-scale models is facing a broad range of issues. For instance, large state spaces (e.g. due to high resolution in spatial dimensions) and structural complexities (e.g. due to nonlinearities in reaction rate equations) often lead to expensive or even infeasible model evaluations for simulation and optimization studies. To mitigate these issues, we use POD-DEIM to generate fast and accurate surrogate models, suitable for many applications.
Model order reduction (MOR) seeks to derive low-dimensional reduced models (ROMs) which are less complex, allowing us to do faster and more robust simulations. Trajectory-based MOR techniques, such as POD-DEIM, have been widely applied to nonlinear systems to obtain these ROMs via projection of the original system using its dominating POD basis [1].
To estimate the potential of nonlinear MOR for catalytic reactors, a process model for methanation is examined exemplarily. For instance, such a process is used to convert renewable hydrogen, coming from electrolysis, to more easily distributable methane. Therefore, we consider a tubular catalytic wall reactor, as illustrated in the figure below. A semi-descritized dynamic reactor model is constructed by mass and energy balances over an arbitrary control volume. This leads to a large-scale nonlinear ODE system, which is capable of describing the dynamics of the entire reactor interior with respect to the concentration of each component as well as temperature.
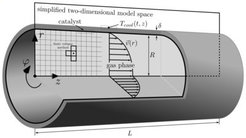
Since, even a single reactor simulation is a computationally cumbersome, the integration of the FOM in various applications, such as optimization and control, becomes a challenging task. However, we employ POD-DEIM on the system to obtain ROMs which can speed up the simulations by several orders of magnitute.
References
-
S. Chaturantabut, and D. Sorensen, Nonlinear Model Reduction via Discrete Empirical Interpolation, SIAM J. Sci. Comput. 32 (5) 2737-2764, 2010.
