Reduced Basis Methods for Electromagnetic Problems
Parametric Model Order Reduction (PMOR) techniques are required in many-query and real-time scenarios, like uncertainty quantification for instance. The Reduced Basis Method as a PMOR technique is applied to problems arising from electromagnetic field simulations of semiconductor structures under the variation of frequency, geometry (e.g. feature size width) and material parameters (e.g. permittivity, permeability).
The Reduced Basis Method (RBM) in electromagnetics shows the potential to enable real-time and many-query tasks of large-scale models, which would not be possible without model reduction.
The main focus of this work are microwave devices. The RBM shows exponential convergence in the approximation error, such that low-order models of high accuracy are generated, even in the case of resonant behavior.
The parameter studies cover the RBM using bounds on the error in the state and expanded formulation methods giving bounds on the output. The electromagnetic components considered are excited by ports, i.e. parts of the structure where external sources such as voltages and currents are applied. The transfer function is then given as the ratio between output and input signals.
Furthermore, an accurate lower bound of the inf-sup stability constant is required for rigorous error estimation. We show and compare multiple techniques for obtaining rigorous and non-rigorous bounds to the stability constant. As resonant parameter configurations can be captured by the stability constant, this information can potentially be used a priori in the construction of the reduced model. Novel bounds are developed, which take information of multiple eigenvalues at a single parameter configuration into account.
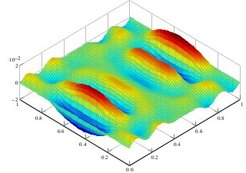
An important task towards more physically accurate parameter settings involve uncertain parameters, since model behavior can often only be quantified with respect to statistical quantities. The uncertainty quantification by Monte-Carlo and stochastic collocation is performed on the time-harmonic microwave model of a coplanar waveguide and a time-dependent dispersion model. The POD-Greedy method is used for the time-dependent model and stochastic collocation to quantify statistical quantities. The figure below shows the first POD mode of the electric field in one spatial component. Again, exponential convergence of the RBM can be observed, when having two dispersion parameters in the model. This allows to use a low-order model in the uncertainty quantification.
Relevant Publications:
M. Hess and P. Benner, Fast Evaluations of Time-Harmonic Maxwell's Equations Using the Reduced Basis Method, IEEE Transactions on Microwave Theory and Techniques, 2013, volume 61, issue 6, pages 2265 - 2274.
M. Hess and P. Benner, A Reduced Basis Method for Microwave Semiconductor Devices with Geometric Variations, COMPEL - The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2014, volume 33, issue 4, pages 1071 - 1081.
M. Hess, S. Grundel and P. Benner, Estimating the Inf-Sup Constant in Reduced Basis Methods for Time-Harmonic Maxwell's Equations, IEEE Transactions on Microwave Theory and Techniques: accepted for publication, 2015.
M. Hess and P. Benner, Reduced Basis Modeling for Uncertainty Quantification of Electromagnetic Problems in Stochastically Varying Domains, 10th International Conference on Scientific Computing in Electrical Engineering, Springer Series "Mathematics in Industry": accepted for publication, 2015.
