Fundamentals
An essential goal of modeling chromatographic processes is to describe the dynamics of concentration and temperature fronts traveling through chromatographic columns. Instructive models originate from differential mass balances for the fluid and solid phases. Model reduction based on evaluating just a limited number of moments of the profiles is known to be a powerful tool to simplify the description of band profiles.
We applied the well-established method of moments for different standard models. Then the method is extended to evaluate more complex and realistic column models. The cases of applying columns packed with core-shell particles, the quantitative description of radial concentration profiles and the propagation of temperature perturbations are analyzed.
References
Rajendran, A., Maruyama, R. T., Rubiera Landa, H. O., & Seidel-Morgenstern, A. (2020). Modelling binary non-linear chromatography using discrete equilibrium data. Adsorption, 26, 973-987.
David, U. U., Qamar, S., & Seidel-Morgenstern, A. (2018). Analytical and numerical solutions of two-dimensional general rate models for liquid chromatographic columns packed with core–shell particles. Chemical Engineering Research and Design, 130, 295-320. doi:10.1016/j.cherd.2017.12.044.
Qamar, S., Kiran, N., Anwar, T., Bibi, S., & Seidel-Morgenstern, A. (2018). Theoretical Investigation of Thermal Effects in an Adiabatic Chromatographic Column Using a Lumped Kinetic Model Incorporating Heat Transfer Resistances. Industrial and Engineering Chemistry Research, 57(6), 2287-2297. doi:10.1021/acs.iecr.7b04555.
Qamar, S., Sattar, F. A., Batool, I., & Seidel-Morgenstern, A. (2017). Theoretical analysis of the influence of forced and inherent temperature fluctuations in an adiabatic chromatographic column. Chemical Engineering Science, 161, 249-264. doi:10.1016/j.ces.2016.12.027.
Qamar, S., Uche, D. U., Khan, F. U., & Seidel-Morgenstern, A. (2017). Analysis of linear two-dimensional general rate model for chromatographic columns of cylindrical geometry. Journal of Chromatography A, 1496, 92-104. doi:10.1016/j.chroma.2017.03.048.
Ahmed, M., Zainab, Q. U. A., & Qamar, S. (2017). Analysis of One-Dimensional Advection–Diffusion Model with Variable Coefficients Describing Solute Transport in a Porous medium. Transport in Porous Media, 118(3), 327-344. doi:10.1007/s11242-017-0833-0.
Qamar, S., Perveen, S., & Seidel-Morgenstern, A. (2016). Numerical approximation of nonlinear and non-equilibrium two-dimensional model of chromatography. Computers and Chemical Engineering, 94, 411-427. doi:10.1016/j.compchemeng.2016.08.008. 235-247.
Qamar, S., Akram, N., & Seidel-Morgenstern, A. (2016). Analysis of general rate model of linear chromatography considering finite rates of the adsorption and desorption steps. Chemical Engineering Research and Design, 111, 13-23. doi:10.1016/j.cherd.2016.04.006.
Qamar, S., Sattar, F. A., Abbasi, J. N., & Seidel-Morgenstern, A. (2016). Numerical simulation of nonlinear chromatography with core–shell particles applying the general rate model. Chemical Engineering Science, 147, 54-64. doi:10.1016/j.ces.2016.03.027.
Qamar, S., & Seidel-Morgenstern, A. (2016). Extending the potential of moment analysis in chromatography. Trends in Analytical Chemistry, 81, 87-101. doi:10.1016/j.trac.2016.01.007.
Ideal Adsorbed Solution Theory
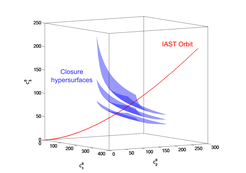
Several theories have been developed in the last decades attempting to describe multicomponent adsorption. One of these theories, based upon classical chemical thermodynamic arguments, is Ideal Adsorbed Solution Theory (IAST).
Our research in this field has been a fruitful and successful enterprise with the Systems and Control Theory group of our institute (Prof. Dietrich Flockerzi).
This cooperation has led to the development of a robust generalized solution concept applicable to an N component system with nondecreasing single component adsorption isotherms.
Dynamic simulation of fixed-bed adsorbers
A very attractive feature of these achievements consists in overcoming time-consuming calculations by a sound mathematical understanding of the features of the IAST model. This results in robust and reliable implementations of the adsorption equilibrium computation for the dynamic simulation of liquid chromatography multi-column arrangements, e.g., SMB.
To this purpose, we implement suitable numerical schemes to solve the partial differential equations that describe fixed-bed adsorbers. We perform the necessary local adsorption equilibrium calculations with the efficient procedures.
This is one of several on-going topics within our research scope.
References
Mutavdzin, I., Seidel-Morgenstern, A., Petkovska, M., (2013). Estimation of competitive adsorption isotherms based on nonlinear frequency response experiments using equimolar mixtures–numerical analysis for racemic mixtures. Chemical Engineering Science, 89, 21-30.
Rubiera Landa, H. O., Flockerzi, D., Seidel-Morgenstern, A., (2013). A method for efficiently solving the IAST equations with an application to adsorber dynamics. AIChE-Journal, 59 (4), 1263-1277.
Rubiera Landa, H.O., Flockerzi, D., Seidel-Morgenstern, A., (2013). „A method for efficiently solving the IAST equations with an application to adsorber dynamics“ AIChE Journal, 59 (4), 1263-1277.
Heinonen, J., Rubiera Landa, H.O., Sainio, T., Seidel-Morgenstern, A., (2012). „Use of Adsorbed Solution theory to model competitive and co-operative sorption elastic ion exchange resins” Separation and Purification Technology, 95, 235-247.
